Risque systémique solaire, tremblements de terre et loi de puissance

Les échelles mesurant le risque solaire sont-elles adaptées ?

Un point m’intriguait depuis un moment : essayer de préciser le degré criticité du risque lié aux éruptions solaires par rapport à d’autres formes de risques environnementaux connus. En particulier par rapport au risque sismique qui a été suivi et éprouvé depuis longtemps par l'homme.

A contrario, le risque solaire est mal connu, tout du moins en regard des effets destructeurs qu'il pourrait provoquer sur notre société actuelle.

Le fait est que notre société, en l'espace d'à peine deux décennies, est devenue extrêmement dépendante de ses moyens d'information et de communication: son activité socio-économique repose massivement sur les moyens d'information et communication qui irriguent la planète: tout s'est "virtualisé".

Or, cette société qui émerge à peine de son enfance n'a guère eu pour l'instant l'occasion de vivre "l'épreuve du feu", c'est à dire de faire face à des événements électromagnétiques d'ampleur, et nous devrions y être particulièrement vigilants.

En l’occurrence, le fait qu’en l’espace d'à peine 20 ans nous ayons eu par deux fois des événements qui dépassaient l’échelle d’évaluation du flux de rayonnement X émis par le soleil (exprimés en watts / m²) était intriguant : soit cette échelle est très mal calibrée, auquel cas nous sommes loin d’avoir vu le pire (!), soit nous avons eu effectivement à faire à des éruptions excessivement rares et exceptionnelles.

Cet article montre que nous sommes, apparemment, loin d'avoir tout vu.

Échelles de mesure de l'activité solaire (National Oceanic and Atmospheric Administration, USA)

Il existe principalement trois échelles et la plus connue d'entre elles classe le flux solaire selon l'intensité de l'énergie reçue au voisinage de la terre, exprimée en Watts par mètres carrés et mesurée dans la bande de rayonnement X de 1 à 8 Ångström. La collecte des données est réalisée en continu par des satellites du programme américain GOES X-ray (Geostationary Operational Environmental Satellite). A ces mesures, en W.m^-2, on fait correspondre une échelle qui s’exprime sous la forme de différentes classes nommées A, B, C, M et X. Ce qui offre, en pratique, une lecture simple et accessible de l'ordre de grandeur du flux solaire :

Classe de l'éruption	Flux, mesuré dans l'intervalle 0.1-0.8 nm exprimé en W·m-2	Echelle comparée des Blackouts Radio
	I > = 10-3	R5 = X20 R4 = X10
X	I > = 10-4	R3 = X1
M	10-5 < = I < 10-4	R2 = M5 R1 = M1
C	10-6 < = I < 10-5	-
B	10-7 < = I < 10-6	-
A	I < 10-7	-

Chaque classe correspond à une éruption solaire d'une intensité dix fois plus importante que la précédente, où la classe X correspond aux éruptions solaires ayant une intensité de 10^-4 W/m². C'est donc une échelle logarithmique, à l'instar sur Terre de l'échelle de Richter. Cette classification est nécessaire car l'énergie des éruptions peut couvrir plusieurs degrés de magnitude suivant une distribution de la fréquence des éruptions proportionnelle à l'inverse de l'énergie totale émise.

Au sein d'une même classe, les éruptions solaires sont numérotées de 1 à 10 selon une échelle linéaire (ainsi, une éruption solaire de classe X2 est deux fois plus puissante qu'une éruption de classe X1, et 4 fois plus puissante qu'une éruption de classe M5).

L'échelle utilisée pour le soleil semble aisément pouvoir être dépassée ...

Cette échelle est ouverte. Or, comme je le soulignais précédemment, deux des plus puissantes éruptions solaires qui ont été enregistrées par les satellites du programme GOES, le 16 août 1989 et le 2 avril 2001, étaient de classe X20 (2 mW/m2). Soit déjà bien au-delà du X10 qui marque la "fin" de l'échelle initialement envisagée. Elles ont été elle-mêmes surpassées le 4 novembre 2003, par l'éruption la plus importante jamais enregistrée, estimée à X28 (heureusement pas dirigée vers la Terre).

Ces mesures s'étalant sur 20 ans, cela ne représente qu'à peine le temps de deux battements de coeur à l'échelle de vie de notre soleil. Et pour le record de 2003: autant dire que c'était hier. C'est dire le peu de recul que nous avons sur cette échelle et sa pertinence.

En limite du limbe solaire le 04 Novembre 2003 à 19h50 UT, la tache 0486 a saturé à X17.4 les détecteurs de rayons X du satellite GOES chargé de la surveillance du Soleil. Le satellite a été aveuglé pendant 11 minutes. L'éclat a été reclassifié quelques jours plus tard en X28 mais quelques chercheurs pensent que l'éclat a avoisiné les X40. Heureusement pour la Terre, l'éjection n'était pas directement dirigée vers celle-ci ! Les relevés de mesure réalisés par le programme GOES X-Ray sont accessibles en quasi-temps réel. Une synthèse sur cette page

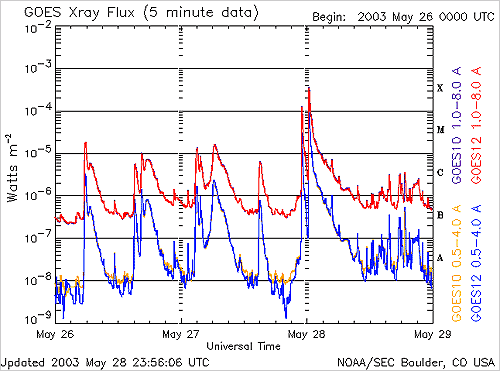
Il est difficile (par manque de recul) d'évaluer l'impact que pourrait avoir une éruption solaire en fonction de sa puissance, néanmoins nous pouvons essayer d'en avoir une petite idée en fonction d'éléments déjà connus:

X20	Le 13 mars 1989, à 2 h 46 du matin, un orage magnétique de forte intensité provoque une coupure d'électricité qui dure près de 9 heures et paralyse le Québec. Des départs de feu sont également signalés. Les pertes provoquées par cet événement furent estimées à plusieurs centaines de millions d’euros.
X28	L'explosion solaire du 04 Novembre 2003 a saturé les détecteurs du satellite GEOS chargé de sa surveillance. Heureusement, celle-ci n'était pas dirigée vers la Terre! Observez qu'une éruption de forte intensité ne se produit pas nécessairement lors d'une phase d'activité importante du point de vue des tâches solaires.
X40-X50	Le 28 août 1859 le ciel du globe devient rouge jusqu'aux latitudes les plus basses. L'éruption de 1859 n'a pas pu être directement mesurée mais a laissé des traces dans les glaces du Groenland et a été catégorisée entre X40 et X50, correspondant à une énergie comprise entre 4 mW/m2 et 5 mW/m2.
>X200	La terre "s'arrête", le black-out est total: plus d’Internet, plus de télécoms, plus de GPS, plus d’électricité, les avions tombent, les voitures, les ascenseurs se bloquent, etc... Destruction totale de l'infosphère, de l'économie et de la finance mondiale. La terre s'enveloppe d'une brume acre et poisseuse. La température chute, un petit age glaciaire est à prévoir. Voir le scénario présenté sur ce site.

Probabilité et fréquence des événements de forte intensité

Sommes nous finalement à l'abri d'une catastrophe de grande envergure, sans dire quand cela peut arriver, pouvons nous avoir une idée de la fréquence de tels événements ? Cela revient à se poser la question suivante :

« Quelle fonction de répartition approxime la fréquence des éruptions solaires en fonction de leur degré de puissance/d’intensité ? » 

Fonctions de répartition de la densité de probabilité: loi de puissance et loi normale

Nous avons là un phénomène dont la puissance suit une courbe logarithmique, à l'inverse de sa fréquence.

Ce type de répartition correspond à une classe de phénomène dont la densité de probabilité peut-être approximée par une loi de puissance du type y=10^b.x^a. La classe de phénomènes décrite par des lois de puissance correspond à des événements potentiellement extrêmes :

• les catastrophes humaines ou naturelles (les ouragans, tremblements de terre, inondations ou crues, la gravité des incendies de forêt, les guerres par le nombre de morts au combat...)
• le domaine économique (avec les crises financières/krachs et chocs pétroliers, ...)
• L'astronomie avec la répartition des planètes, leurs périodes de révolution, le diamètre des cratères lunaires, etc.
• La dynamique des populations (taille des villes, nombre d’espèces par genre chez les mammifères, ...)
• La structure de l'information (sur Internet avec le nombre de liens pointant sur une page internet, la taille des fichiers qui circulent sur un réseau, le taux de fréquentation d’une page donnée, la fréquence des mots, ...)
• etc

La période des planètes peut s'exprimer suivant une loi de puissance de même que leur distance au soleil, ce qui est logique, ces deux valeurs étant reliées par la formule : . La pente de ce graphe exprime immédiatement le rapport de puissances existant entre la période sidérale T des planètes et le demi-grand axe a de leurs trajectoires, et sa valeur est a = 2/3

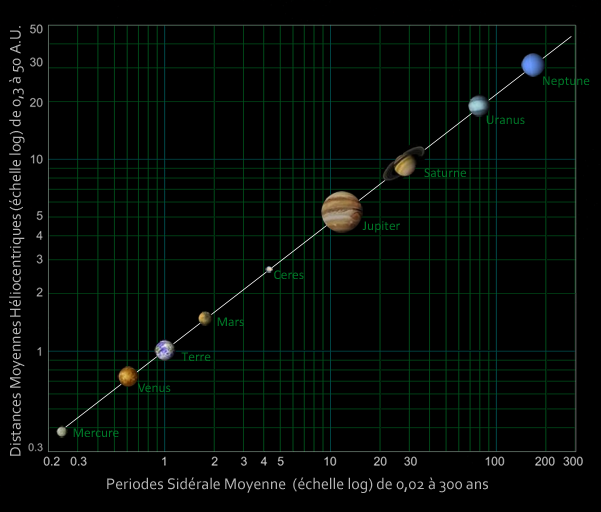
Les exemples sont innombrables et il s'agit d'un champ de recherches particulièrement actif, notamment par l'importance de son impact socio-économique (voir la Théorie des Valeurs Extrêmes ou "TVE"): en fait, la distribution des changements dans un système complexe suit usuellement une loi de puissance.

La première loi de puissance historiquement reconnue a été fournie dans le domaine économique par Vilfredo Pareto (justement appelée "loi de Pareto" ou des "80/20"): il a ainsi remarqué que 20% de la population possédait 80% des richesses de son pays… En effet, en projetant sur un papier log/log la répartition des richesses de son pays par famille il s'est aperçu que cette répartition suivait une droite à partir d'un rang X₀ choisi  :

Un point sur lequel l'on insiste pas assez à propos de la loi de puissance ou de Pareto, c'est qu'elle ne constitue qu'une approximation d’une distribution dont nous ignorons en réalité l'équation réelle. Ainsi, la loi de Pareto montre ses limites: elle ne fonctionne bien qu’à partir d’un certain rang X₀ et jusqu’à un certain degré d’erreur acceptable :
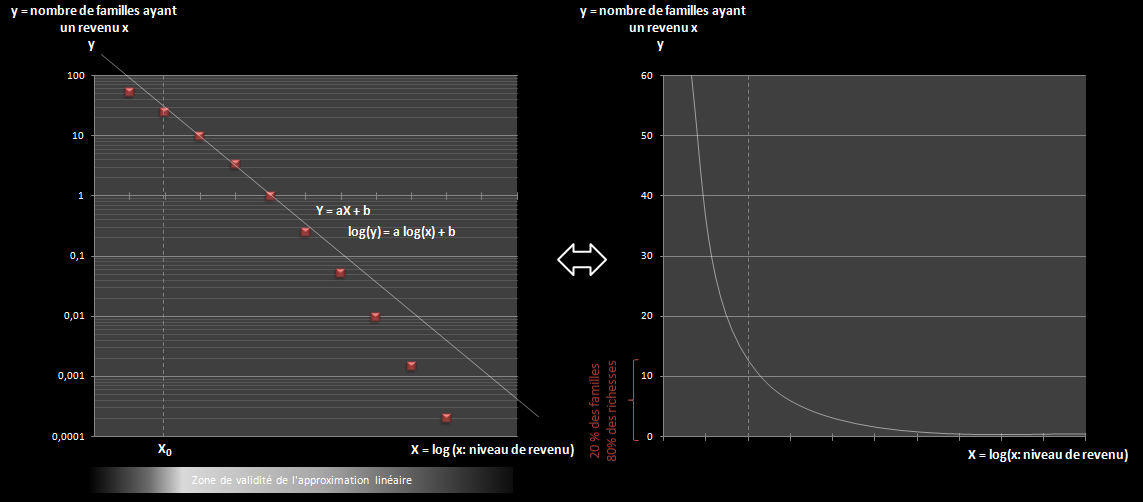
* lorsque X tend vers l’infini les résultats deviennent de plus en plus mauvais.
* Lorsque X<X₀ les résultats sont carrément mauvais.
Si la loi de Pareto s'écrit sur une échelle log/log sous la forme d'une équation linéaire Y=aX+b (avec Y=log(y) et X=log(x)), alors il est déjà possible d'avoir une meilleure approximation de la distribution qu'elle approche ne serait-ce qu'en réalisant sur ce même graphe une approximation avec une équation du second degré Y = aX²+bX+c soit y = 10^cx^{a log(x) +b}

On remarquera que cette loi a un pendant, lorsque la densité de probabilité se répartit de façon symétrique autour d'un axe (point de densité de probabilité maximal), il s'agit de la loi normale (ou courbe de gauss). A dire vrai, il y a un lien entre les deux types de loi (loi normale et loi de puissance): toutes deux représentent des classes de phénomènes qui de populations de variables font émerger des paramètres liés à la distribution de leurs valeurs.

De la première les scientifiques disent qu'il s'agit d'une loi à « longue traine » (permettant d'observer des phénomènes rares jusqu'à de très grandes échelles de puissance), contrairement à la seconde qui décroit beaucoup plus rapidement et « étouffe » toute chance d'observer un phénomène à très grande valeur de X.

Modélisation comparée pour le soleil et les tremblements de terre

Pour le soleil, différentes modélisations sont possibles en fonction des valeurs mesurées que l'on choisi. Ainsi, le NOAA propose 3 échelles de risque, chacune décrivant des effets environnementaux différents :

1. les tempêtes géomagnétiques: échelle de G1 à G5.

• Mesure la force champ magnétique terrestre indice Kp il dépend à la dois de la force du vent solaire et du comportement de la dynamo terrestre. L'indice Kp suit une courbe quasi logarithmique, il est exprimé en correspondance de plages de valeurs en nano-Teslas (de 0 à 9: 0, 5, 10, 20, 40, 70, 120, 200, 330, et plus...).

2. Les tempêtes de radiation solaires: échelle de S1 à S5.

• Mesure la force des radiations solaires. Il s'agit d'une mesure du flux d'ions reçu en s^-1·ster^-1·cm^-2.

3. Les "blackout" radio: échelle de R1 à R5, en correspondance avec l'échelle A, B, C, M, X, ... remarque, au passage, l'échelle des R n'est curieusement pas logarithmique : R1=M1 et R2=M5 ou R4=X10 et R5=X20...

• Mesure le flux de rayons X (0.1-0.8 nm) en W·m^-2

Les données sont consolidées dans des tableaux. Concernant les tremblements de terre les informations sont extraites d'une base de données de l'USGS : les tremblements de terre d'échelle 6 à 9 et entre 1973 et 2009 ont été retenus.

Dans les tableaux précédents, les événements sont comptabilisés sur une période de 11 ans (moyenne sur 11 ans pour les tremblements de terre). Maintenant, si l'on projette l'ensemble des échelles avec leurs densités de probabilité liées, nous obtenons ce graphique surprenant:

Le soleil étant le générateur commun à ces trois échelles de puissance, logiquement, l'on pouvait s'attendre à observer de fortes corrélations entre ces lois. Et la relation parait immédiate dans le cas de l'évolution comparée en fréquence des tempêtes géomagnétiques et des radiations solaires: les "droites" d'approximations sont quasi-parallèles (attention! elles ne paraissent ici "droites" que parce que nous sommes en échelle log/log).

Néanmoins, si ce résultat était attendu pour le soleil, il est - à priori - surprenant de voir que les tremblements de terre sont régis par une loi de puissance de même ordre que celle des blackouts radios !

Et le décalage latéral sur l'axe X ne constitue pas un point gênant en tant que critère de comparaison: l'évaluation relative de la puissance des phénomènes dépend fortement des unités de mesure utilisées dans leur calcul ainsi que du positionnement, souvent arbitraire pour le "niveau 1" de puissance de chaque échelle (il s'agit généralement d'un critère "d'observabilité").

Relation entre les différents types d'événements

Dans un graphe ou Y = log(y) X = log(x), il est possible d'exprimer ces fonctions sous la forme d'équations linéaires paramétrées du type Y = aX + b ou a est la pente de la droite. Dans le graphique ci-dessus, les approximations sont calculées par excel et affichées sous la forme de courbes de tendance de nature exponentielle. Ces fonctions peuvent s'écrire de façon strictement équivalente sous la forme d'une fonction du type y = 10^b e^{a' X} = 10^b e^{a ln(x)} = 10^b x^a = b' x^a...

Il faut comprendre que les valeurs des pentes des droites d'approximation, sont liées aux facteurs de puissance appliqués aux différents paramètres des équations permettant de calculer la puissance effective des phénomènes considérés. Par exemple la décroissance en 1/r² du champ gravitationnel serait affublée d'une pente de valeur -2. Il s'agit normalement de valeurs "simples" liées aux dimensions exprimées (rapports de puissance). En d'autres termes, on peut supposer des rapports entiers entre les pentes des droites. Or, vérification faite, nous avons:

a2 = 3.a1 à 10-2 près, avec,
- a1 la pente moyenne pour les événements de type orage électromagnétiques et radiations solaires
- a2 la pente moyenne pour les événements de type black out radio et tremblements de terre.

Ce résultat peut s'énoncer comme suit :

- L’augmentation de fréquence des événements liés aux orages géomagnétiques évolue 
  en puissance de 3 par rapport à ceux liés aux blackout radio, ou bien,
- L’augmentation de fréquence des événements liés aux radiations solaires évolue 
  en puissance de 3 par rapport à celle liée aux tremblements de terre...
- etc.

Il est possible de synthétiser ces résultats suivant un petit graphe relationnel :

Il est tout à fait logique que le paramètre a1 s'applique à l'échelle de mesure des tempêtes géomagnétiques ET des tempêtes de radiations solaires, car il dépend du même type de phénomène sous-jacent, le flux d’ions et de protons porté par les vents solaires. L'on observe au passage que l'augmentation de la puissance des tempêtes géomagnétiques ne doit apparemment rien à des paramètres géologiques, même si localement, la Terre influence les valeurs localement mesurées pour K_p.

Une relation entre le soleil et les tremblements de terre ?

Attention aux raccourcis trompeurs : ce n'est pas parce que des lois de puissance sont corrélées que les phénomènes qu'elles représentent sont nécessairement liés par des lois de cause à effet.

Toutefois, dans le cas présent, au moins deux effets peuvent être proposés afin d'expliquer une relation entre les tremblements de terre et le soleil. Ils dépendent tous deux de la masse du Soleil et de sa distance à la Terre.

• Le premier, est du à un effet de marée provoqué par le Soleil sur la Terre (ainsi que la Lune): il déforme la Terre faisant d'elle un ellipsoïde. Ce phénomène provoque des tensions importantes dans le sous-sol terrestre: il échauffe le magma et s'accompagne de phénomènes dissipatifs dont les volcans, les tremblements de terre et les rayonnements de basse longueur d'onde sont des manifestations. Cet effet dépend essentiellement de la latitude: il est quasi nul au pôles, maximal à l'équateur. Or précisément, si l'on observe la répartition des tremblements de terre sur un planisphère :

Ci-dessus, concernant le profil de densité par latitude, utiliser une échelle plus détaillée (par exemple des incréments de 5°) accroitrait un effet de bord : celui de donner plus d'importance aux conditions locales de terrain et cela créerait du bruit par rapport à l'échelle du phénomène que l'on souhaite ici expliciter...

En dessous de 70° de latitude sud il n'y a plus de tremblements de terre ! Voilà aussi pourquoi les tremblements de terre faisant la une de nos actualités sont généralement situés dans des régions situées à des latitudes proches de l'équateur (Haïti, Philippines, etc.). A noter que cet effet de marée est lié à l'inverse du cube de la distance aux astres perturbateurs que sont la Lune et le Soleil. Le soleil, par définition est situé dans le plan de l'écliptique, la lune est inclinée sur ce plan à 5°: grosso-modo les effets des marées de ces deux corps se cumulent, celui de la lune étant 3 fois plus important que celui créé par le soleil.

• Le second effet serait lié à des champs électromagnétique d'extrêmement basse fréquence (ELF). Cet effet est moins bien connu et est toujours étudié: le vent solaire induirait des courants variables de basse fréquence responsables de l'injection en sous-sol de grandes quantités d'énergie. Ce rayonnement serait susceptible de libérer des tensions le long des failles à l'origine des tremblements de terre. En effet, les très basses longueurs d'onde sont capables de pénétrer profondément dans le sol, ce d'autant plus que les conditions de terrain s'y prêtent.

Des études menées à partir de stations au sol, qui enregistrent les émissions d'ondes ELF/VLF reçues, ont permis d'observer des cycles dépendants de l'insolation ET de l'activité solaire. Notamment:

• 1 cycle quotidien d'activité (avec un maximum vers midi),
• 1 cycle de 27 jours,
• 1 cycle d'un an, (compte tenu de l'inclinaison de la Terre sur son axe),
• et 1 cycle de 11 ans, lié aux cycles d'activité du soleil...

Ces courants sont générés essentiellement dans les régions des arcs auroraux: là où le champ géomagnétique terrestre plonge vers la terre et permet aux vents solaires de se rapprocher des zones les plus denses de l'atmosphère, créant ainsi des nuages électroniques à l'origine de ces courants. Sous réserves, ils pourraient être à l'origine d'une activité sismique et volcanique accrue à 60° de latitude nord et 60° sud de la planète, participant à la création des bourrelets observables dans la distribution des séismes en haute et basse latitude (par exemple, au niveau de la ceinture de feu nord et sud du pacifique):

Le champ électromagnétique de très basse longueur d'onde au niveau du sol terrestre n'a été que peu étudié depuis l'espace. Le satellite franco-russe AUREOL 3 dont une carte à 800 Mhz est présentée ci-dessus, date de 1981, le satellite DEMETER lancé en 2004 a depuis repris le flambeau : il est notamment chargé de détecter les signaux électromagnétiques préludant et succédant aux séismes. Néanmoins, encore beaucoup de données restent à dépouiller de ce satellite...Ci dessus, les ondes à très basse fréquence n'auraient qu'un effet plus mineur sur les tremblements de terre et les volcans : elles amplifieraient localement l'action des forces de marée dues à la gravitation mais ne seraient pas capables à très basse (resp. haute) latitude d'engendrer un effet notable à elles seules. La forme légèrement sinusoïdale de ces bandes à basses fréquences est dûe à la configuration du champ géomagnétique terrestre : à l'emplacement des pôles nord & sud magnétique terrestre le champ magnétique terrestre est suffisamment intense pour repousser les particules chargées en sa périphérie (à l'image de l'oeil d'un cyclone). A noter que les relevés d'AUREOL 3 ci-dessus sont valables pour la seule année 1981, alors que les tremblements de terre affichés correspondent à 36 ans de relevés : sachant que le champ géomagnétique terrestre varie chaque année la superposition souffre nécessairement d'imprécision! Pour poursuivre la réflexion sur la base du schéma ci-contre, différentes études traitent de la question des ondes ELF/VLF induites par le soleil, par exemple: * Quasi-periodic ELF/VLF wave emissions in the Earth’s magnetosphere: comparison of satellite observations and modeling * Solar Influence on ELF-VLF Emission Observed at Conjugate Stations * Solar cycle dependence, seasonal and daily variations, and weekend effect deduced from long-term monitoring of ELF/VLF emissions at Syowa-Iceland geomagnetic conjugate stations. * Propagation Characteristics and Generation Mechanism of ELF/VLF Hiss Observed at Low-latitude Ground Station (L = 1.17) etc. Ou bien des particules chargées détectées en haute atmosphère en lien avec l'activité sismique : * Observations of trapped energetic particle precipitations conducted simultaneously from two satellites, Aureol-3 and IKB-1300, over the same earthquake epicenter area prior to the main shock are reported. Of the 20 Aureol-3 flights during which detectable increases were observed in the precipitation of high-energy (greater than 100 keV) electrons and protons, earthquakes of magnitude greater than 4 (Richter scale) were observed in 18 cases at L less than 1.3 from the magnetic equator, with a longitude displacement of +/- 60 deg. Et le programme HAARP qui semble vouloir s'inspirer de ces mécanismes (à des échelles de puissance et d'étendue près): * ce qu'il est possible de faire avec HAARP. Enfin, dans le sens inverse, celui d'une émission d'ondes ELF depuis les zones de faille (roches piezo-électriques qui travailleraient), un programme d'observation est toujours mené avec le satellite DEMETER (ce programme touche à sa fin) : * Detection of Electromagnetic Emissions Transmitted from Earthquake Regions. Etc .

Bref, pour discriminer et faire la part entre les deux mécanismes proposés ci-dessus, il serait intéressant d'étudier s'il existe une corrélation entre les variations de l'irradiation solaire et les tremblements de terre à différentes échelles de temps. Pour avoir superficiellement abordé la question, les cycles diurnes et/ou saisonniers ne semblent pas avoir d'impact. A l'échelle de ces 30 dernières années une faible corrélation existe entre l'accroissement des températures et l'irradiation solaire, mais elle redevient fausse à l'échelle du siècle. La corrélation pourrait peut-être s'avérer pertinente avec les variations de température moyennes sur le globe, mais l'on diverge du sujet...

Mais quid des risques comparés entre les tremblements de terre et le soleil ?

Pour répondre à cette question, il faut pouvoir disposer d'une meilleure approximation de la fréquence des événements, notamment pour des X élevés, ce qui n'est pas le cas avec les approximations linéaires précédentes. D'ailleurs, vous l'aurez peut-être remarqué, je n'ai pas intégré dans celles-ci la dernière valeur fournie pour chacune des échelles de risques solaires:

• d'une part ces valeurs dégradent passablement les coefficients de corrélation des différentes équations affines,
• d'autre part, il n'existe que de rares événements associés à ces valeurs "hautes": respectivement, pour chacune des 3 échelles, 1, 1 et 5 événements comptabilisés sur une période de 11 ans, ce qui statistiquement est fragile.

Toutefois, comme nous souhaitons connaître plus précisément les fréquences des événements lorsque ceux-ci deviennent rares et extrêmes, il serait juste d'essayer de disposer d'une meilleure fonction d'approximation pour des X élevés. Nous nous proposons donc d'utiliser une équation du second degré. Toutefois, ce que cette équation va nous faire gagner sur des X grands, nous le perdrons en précision "générale" et compte tenu de l'incertitude statistique sur les points ajoutés.

Nous vérifions effectivement que les coefficients de corrélation sont tous (légèrement) dégradés, sauf pour les tremblements de terre où il devient égal à 1 (=> la période de suivie est plus longue, les statistiques sont plus fiables, seuls 4 points sont corrélés ce qui avec une équation du second degré facilite l'opération!)

Ce qui sous la forme d'un graphe log / log donne:

Ci dessus à droite, les rectangles colorés indiquent les échelles de puissance prévues par le NOAA (en rouge/orange/violet) en comparaison de l'échelle de Richter : elles sont très réduites !

Il apparait ici clairement que les événements de nature solaire peuvent atteindre des niveau de puissance outrepassant largement les échelles conçues pour les suivre.

Certes les échelles sont ouvertes, mais il parait irresponsable de ne pas les faire coller à la réalité, et de ne pas anticiper l'impact que serait susceptible d'avoir une éruption solaire majeure. Car, si une idée grossière des effets auxquels nous pouvons nous attendre en fonction de la puissance des événements est bien fournie sur le site du NOAA, celle-ci est évoquée uniquement pour des événements couverts par leurs échelles !

Du côté des séismes, si les hautes valeurs de l'échelle de Richter ne sont que rarement atteintes (voire jamais à l'échelle humaine pour les puissances d'ordre 10, 11 et 12), malgré tout, les événements les plus puissants relevés, outrepassent -à fréquence égale- les événements solaires les plus remarquables discutés sur la toile: voir le graphique ci-après.

Comparaison des échelles sismiques et solaires suivant les périodes associées à leur degré de puissance

Pour plus de clarté, nous pouvons projeter ces informations sur un simple graphe à partir des périodes:

Ce résultat est édifiant:

A l'échelle, ne serait-ce que de 250 années, la Terre est susceptible de subir un événement solaire 100 fois plus intense que ce que nous avons déjà connu ces 20 dernières années, que ce soit en termes de radiations solaires ou bien d'orages magnétiques, et d'ordre 10 fois supérieur en rayonnement X.

Et pour un événement survenant une fois tous les 10 000 ans, serions nous prêts ?

La réponse est clairement, NON.

Rappelons qu'à l'inverse d'un tremblement de terre, un événement du type solaire aurait un impact d'ordre mondial.