Difference between revisions of "Loi normale"
| (3 intermediate revisions by the same user not shown) | |||
| Ligne 1: | Ligne 1: | ||
| − | Cette courbe est aussi appelée loi de Gauss, | + | Cette courbe est aussi appelée loi de Gauss, (mathématicien allemand Karl Friederich Gauss (1777-1855)). |
| − | La loi normale représente l'espace de révolution de phénomènes "aléatoires". | + | La loi normale représente l'espace de révolution de phénomènes "aléatoires", classiquement l'on parle de <b>densité de probabilité</b>. |
De nombreuses autres lois statistiques peuvent être approchées par la loi normale, tout spécialement dans le cas des grands échantillons. | De nombreuses autres lois statistiques peuvent être approchées par la loi normale, tout spécialement dans le cas des grands échantillons. | ||
| Ligne 14: | Ligne 14: | ||
* n le nombre total d'individus dans l'échantillon | * n le nombre total d'individus dans l'échantillon | ||
* n(x) le nombre d'individus pour lesquels la grandeur analysée a la valeur x. | * n(x) le nombre d'individus pour lesquels la grandeur analysée a la valeur x. | ||
| + | |||
| + | note: il existe aussi des répartitions non symétriques. | ||
Latest revision as of 11:27, 25 octobre 2005
Cette courbe est aussi appelée loi de Gauss, (mathématicien allemand Karl Friederich Gauss (1777-1855)).
La loi normale représente l'espace de révolution de phénomènes "aléatoires", classiquement l'on parle de densité de probabilité.
De nombreuses autres lois statistiques peuvent être approchées par la loi normale, tout spécialement dans le cas des grands échantillons.
Son expression mathématique est la suivante:
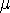est la moyenne,
l'écart type.- n le nombre total d'individus dans l'échantillon
- n(x) le nombre d'individus pour lesquels la grandeur analysée a la valeur x.
note: il existe aussi des répartitions non symétriques.
