Solar systemic risk, earthquakes and power laws
Sommaire
Are the scales measuring solar risk appropriate?
One point has intrigued me for a while: trying to specify the degree of criticality of the risk linked to solar flares in relation to other forms of known environmental risks. In particular compared to the seismic risk which was followed and tested for a long time by the man.
On the contrary, the solar risk is not well known, at least with regard to the destructive effects that it could cause on our current society.
The fact is that our society, in the space of barely two decades, has become extremely dependent on its means of information and communication : its socio-economic activity is massively based on the means of information and communication which irrigate the planet: everything has become "virtualized".
However, this society which is barely emerging from its childhood has hardly had the opportunity for the moment to live "the test of fire", that is to say to face electromagnetic events of magnitude, and we should be particularly vigilant about it.
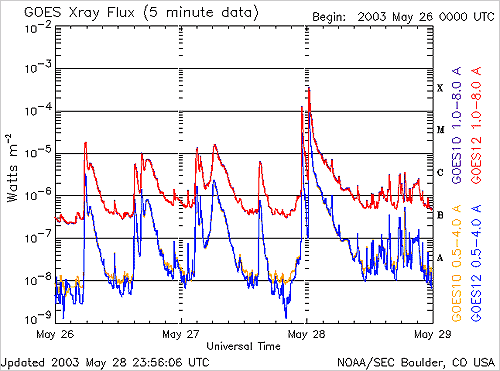
In this case, the fact that in the space of barely 20 years we have twice had events that exceeded the scale for evaluating the flux of X-radiation emitted by the sun (expressed in watts / m 2 ) was intriguing: either this scale is very badly calibrated, in which case we are far from having seen the worst (!), or we actually had to deal with excessively rare and exceptional eruptions.
This article shows that we are, apparently, far from having seen everything.
Solar activity measurement scales (National Oceanic and Atmospheric Administration, USA)
There are mainly three scales and the best known of them classifies the solar flux according to the intensity of the energy received in the vicinity of the earth, expressed in Watts per square meter and measured in the X-radiation band from 1 to 8 Ångström. Data collection is carried out continuously by satellites from the American program GOES X-ray (Geostationary Operational Environmental Satellite). To these measurements, in W.m-2,, we match a scale which is expressed in the form of different classes named A, B, C, M and X. This offers, in practice, a simple and accessible reading of the order of magnitude of the solar flux:
| Eruption Class | Flux, measured in the range 0.1-0.8 nm expressed in W·m-2 |
Comparative Scale of Radio Blackouts |
| I > = 10-3 | R5 = X20 R4 = X10 |
|
| X | I > = 10-4 | R3 = X1 |
| M | 10-5 < = I < 10-4 | R2 = M5 R1 = M1 |
| C | 10-6 < = I < 10-5 | - |
| B | 10-7 < = I < 10-6 | - |
| A | I < 10-7 | - |
Each class corresponds to a solar flare with an intensity ten times greater than the previous one, where class X corresponds to solar flares with an intensity of 10-4 W/m2. It is therefore a logarithmic scale, like the Richter scale on Earth. This classification is necessary because the energy of the eruptions can cover several degrees of magnitude following a distribution of the frequency of the eruptions proportional to the inverse of the total energy emitted.
Within the same class, solar flares are numbered from 1 to 10 according to a linear scale (thus, a solar flare of class X2 is twice as powerful as a flare of class X1, and 4 times more powerful than an M5 class eruption).
The scale used for the sun seems easily to be surpassed...
This ladder is open. However, as I pointed out previously, two of the most powerful solar eruptions which were recorded by the satellites of the GOES program, on August 16, 1989 and April 2, 2001, were of class X20 (2 mW/m2). Is already well beyond the X10 which marks the "end" of the scale initially envisaged. They were themselves surpassed on November 4, 2003, by the most important eruption ever recorded, estimated at X28 (fortunately not directed towards the Earth).
These measurements being spread over 20 years, this represents only the time of two heartbeats on the scale of life of our sun. And for the 2003 record: in other words, it was yesterday. This shows how little perspective we have on this scale and its relevance.
It is difficult (for lack of hindsight) to assess the impact that a solar flare could have according to its power, nevertheless we can try to have a small idea of it according to already known elements:
| X20 | |
| X28 | |
| X40-X50 |  On August 28, 1859 the sky of the globe turns red to the lowest latitudes. The 1859 eruption could not be directly measured but left traces in the ice of Greenland and was categorized between X40 and X50, corresponding to an energy between 4 mW/m2 and 5 mW/m2. |
| >X200 | The earth "stops", the blackout is total: no more Internet, no more telecommunications, no more GPS, no more electricity, planes fall, cars, elevators get stuck, etc... Destruction global infosphere, economy and finance. The earth is shrouded in an acrid, sticky mist. The temperature drops, a small ice age is to be expected. See the scenario presented on this site.. |
Probability and frequency of high intensity events
Are we finally safe from a large-scale disaster, without saying when it can happen, can we have an idea of the frequency of such events? This amounts to asking the following question:
“ What distribution function approximates the frequency of solar flares as a function of their degree of power/intensity? »
Probability Density Distribution Functions: Power Law and Normal Law
We have here a phenomenon whose power follows a logarithmic curve, contrary to its frequency.
This type of distribution corresponds to a class of phenomenon whose probability density can be approximated by a power law of the y=10 b .x a type . The class of phenomena described by power laws corresponds to potentially extreme events:
- human or natural disasters (hurricanes, earthquakes, floods or floods, severity of forest fires, wars by the number of deaths in combat, etc.)
- the economic field (with financial crises/crashes and oil shocks, etc.)
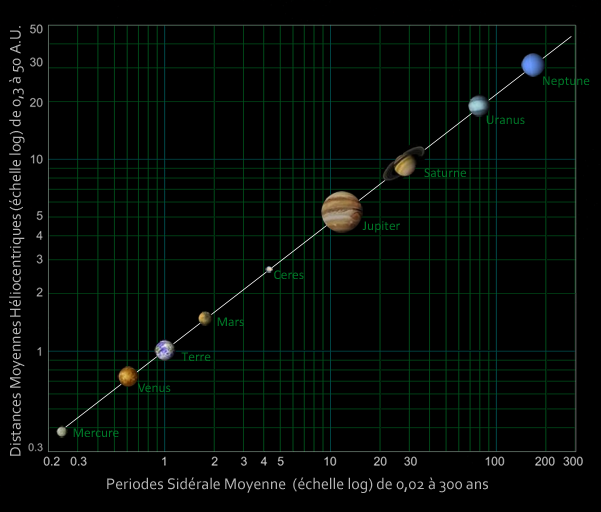
- Astronomy with the distribution of the planets, their periods of revolution, the diameter of the lunar craters, etc.
- Population dynamics (size of towns, number of species per genus in mammals, etc.)
- The structure of information (on the Internet with the number of links pointing to a web page, the size of files circulating on a network, the rate of use of a given page, the frequency of words, etc.)
- etc
The examples are innumerable and it is a particularly active field of research, in particular by the importance of its socio-economic impact (see the Theory of Extreme Values or "TVE"): in fact, the distribution of changes in a complex system usually follows a power law.
The first historically recognized power law was provided in the economic field by Vilfredo Pareto (aptly called "Pareto's law" or "80/20"): he thus noticed that 20% of the population owned 80% of the wealth of his country… Indeed, by projecting on a log/log paper the distribution of the wealth of his country by family, he noticed that this distribution followed a straight line starting from a chosen rank X0 :
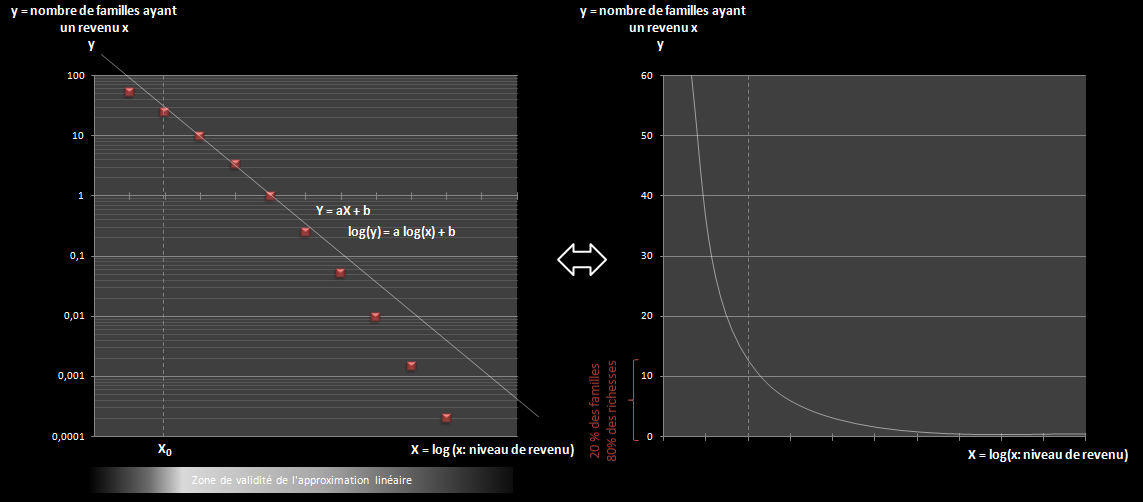
It will be noted that this law has a pendant, when the probability density is distributed symmetrically around an axis (point of maximum probability density), it is the normal law (or Gaussian curve). To tell the truth, there is a link between the two types of law (normal law and power law): both represent classes of phenomena which, from populations of variables, give rise to parameters linked to the distribution of their values.
Of the first, scientists say that it is a "long tail" law (allowing the observation of rare phenomena up to very large scales of power), unlike the second which decreases much more quickly and "stifles" any chance of observing a phenomenon with a very large value of X.
Comparative modeling for the sun and earthquakes
Pour le soleil, différentes modélisations sont possibles en fonction des valeurs mesurées que l'on choisi. Ainsi, le NOAA propose 3 échelles de risque, chacune décrivant des effets environnementaux différents :
1. geomagnetic storms: scale from S1 to S5.
- Mesure la force champ magnétique terrestre indice Kp il dépend à la dois de la force du vent solaire et du comportement de la dynamo terrestre. L'indice Kp suit une courbe quasi logarithmique, il est exprimé en correspondance de plages de valeurs en nano-Teslas (de 0 à 9: 0, 5, 10, 20, 40, 70, 120, 200, 330, et plus...).
2. Solar radiation storms : échelle de S1 à S5.
- Mesure la force des radiations solaires. Il s'agit d'une mesure du flux d'ions reçu en s-1·ster-1·cm-2.
3. The radio blackouts : scale from R1 to R5, in correspondence with the scale A, B, C, M, X, ... note that the Rs scale is curiously not logarithmic: R1=M1 et R2=M5 ou R4=X10 et R5=X20...
- Measures X-ray flux (0.1-0.8 nm) in W·m-2
LThe data is consolidated in tables. Regarding earthquakes, the information is extracted from a USGS database: les earthquakes of scale 6 to 9 and between 1973 and 2009 were retained.
The sun being the generator common to these three scales of power, logically, one could expect to observe strong correlations between these laws. And the relationship seems immediate in the case of the evolution compared in frequency of geomagnetic storms and solar radiation : the "straight lines" of approximations are quasi-parallel (caution! they only appear "straight" here because we are in log/log scale).
Nevertheless, if this result was expected for the sun, it is - a priori - surprising to see that earthquakes are governed by a power law of the same order as that of radio blackouts!
And the lateral offset on the X axis does not constitute a troublesome point as a criterion of comparison: the relative evaluation of the power of the phenomena depends strongly on the units of measurement used in their calculation as well as on the positioning, often arbitrary for the "level 1" power of each scale (this is usually an "observability" criterion).
Relationship between the different types of events
In a graph where Y = log(y) X = log(x), it is possible to express these functions in the form of parameterized linear equations of the type Y = aX + b where a is the slope of the line. In the graph above, the approximationsare calculated by excel and displayed as trendlines that are exponential in nature. These functions can be written in a strictly equivalent way in the form of a function of the type y = 10b ea' X = 10b ea ln(x) = 10b xa = b' xa...
It should be understood that the values of the slopes of the approximation straight lines are linked to the power factors applied to the various parameters of the equations making it possible to calculate the effective power of the phenomena considered. For example the decrease in 1/r 2 of the gravitational field would be decked out with a slope of value -2. These are normally "simple" values related to the expressed dimensions (power ratios). In other words, we can assume integer ratios between the slopes of the lines. However, verification done, we have:
a2 = 3.a1 within 10-2, with, - a1 the average slope for events of electromagnetic storm and solar radiations type, - a2 the average slope for events of radio black out and earthquake type.
This result can be stated as follows:
- The increase in frequency of events related to geomagnetic storms evolves in power of 3 compared to those linked to radio blackouts, or else, - The increase in frequency of events related to solar radiation evolves in power of 3 compared to that related to earthquakes... - etc.
It is possible to summarize these results using a small relational graph:
It is quite logical that the a1 parameter applies to the scale of measurement of geomagnetic storms AND solar radiation storms , because it depends on the same type of underlying phenomenon, the flux of ions and protons carried by solar winds. We observe in passing that the increase in the power of geomagnetic storms apparently owes nothing to geological parameters, even if locally, the Earth influences the locally measured values for Kp.
A relationship between the sun and earthquakes?
Beware of misleading shortcuts: it is not because power laws are correlated that the phenomena they represent are necessarily linked by laws of cause and effect.
However, in the present case, at least two effects can be proposed in order to explain a relationship between earthquakes and the sun. They both depend on the mass of the Sun and its distance from the Earth.
- The first is due to cinetic + tidal effect caused by the rotation of the Earth and the Sun (as well as the Moon): it deforms the Earth making it an ellipsoid. This phenomenon causes significant tensions in the earth's subsoil: it heats up the magma and is accompanied by dissipative phenomena of which volcanoes, earthquakes and low wavelength radiation are manifestations. This effect depends essentially on the latitude: it is almost nil at the poles, maximum at the equator. But precisely, if we observe the distribution of earthquakes on a planisphere:

Below 70° south latitude there are no more earthquakes! This is also why the earthquakes making the headlines in our news are generally located in regions located at latitudes close to the equator (Haiti, Philippines, etc.). Note that this tidal effect is linked to the inverse of the cube of the distance to the disturbing stars that are the Moon and the Sun. The sun, by definition, is located in the plane of the ecliptic, the moon is inclined on this plane at 5°: roughly speaking the effects of the tides of these two bodies are cumulative, that of the moon being 3 times greater than that created by the sun.
- The second hypothetical effect would be related to extremely low frequency (ELF) electromagnetic fields. This effect is less well known and is still studied: the solar wind would induce variable currents of low frequency responsible for injecting large quantities of energy underground. This radiation would be likely to release tensions along the faults at the origin of the earthquakes. Indeed, very low wavelengths are capable of penetrating deeply into the ground and cause seisms.
Studies carried out from ground stations, which record the emissions of ELF/VLF waves received, have made it possible to observe cycles dependent on insolation AND solar activity. Notably:
- 1 daily cycle of activity (with a maximum around noon),
- 1 cycle of 27 days,
- 1 cycle of one year, (taking into account the inclination of the Earth on its axis),
- and 1 cycle of 11 years, linked to the cycles of activity of the sun...
These currents are generated mainly in the regions of the auroral arcs: where the Earth's geomagnetic field dips towards the earth and allows the solar winds to approach the densest areas of the atmosphere, thus creating electronic clouds at the origin of these currents. Subject to reservations, they could be at the origin of increased seismic and volcanic activity at 60° north latitude and 60° south of the planet, participating in the creation of observable bulges in the distribution of earthquakes at high and low latitude ( for example, at the level of the North and South Pacific Ring of Fire):
 The very low wavelength electromagnetic field at ground level has been little studied from space. The Franco-Russian satellite AUREOL 3, an 800 Mhz map of which is shown above, dates from 1981, the satellite DEMETER launched in 2004 has since taken up the torch: it is notably responsible for detecting electromagnetic signals preceding and following earthquakes. Nevertheless, still a lot of data remains to be stripped from this satellite... Above, very low frequency waves would only have a more minor effect on earthquakes and volcanoes: they would locally amplify the action of forces tidal waves due to gravitation but would not be able at very low (resp. high) latitude to generate a notable effect on their own. The slightly sinusoidal shape of these low frequency bands is due to the configuration of the Earth's geomagnetic field: at the location of the earth's magnetic north & south poles, the earth's magnetic field is strong enough to repel charged particles to its periphery (like the eye of a cyclone) . Note that the AUREOL 3 readings above are valid for the year 1981 alone, while the earthquakes displayed correspond to 36 years of readings: knowing that the Earth's geomagnetic field varies each year, the superposition necessarily suffers from inaccuracy! To pursue the reflection on the basis of the diagram opposite, various studies deal with the question of ELF/VLF waves induced by the sun, for example: * Quasi-periodic ELF/VLF wave emissions in the Earth’s magnetosphere: comparison of satellite observations and modeling * Solar Influence on ELF-VLF Emission Observed at Conjugate Stations * Solar cycle dependence, seasonal and daily variations, and weekend effect deduced from long-term monitoring of ELF/VLF emissions at Syowa-Iceland geomagnetic conjugate stations. * Propagation Characteristics and Generation Mechanism of ELF/VLF Hiss Observed at Low-latitude Ground Station (L = 1.17) etc. Or charged particles detected in the upper atmosphere in connection with seismic activity: * Observations of trapped energetic particle precipitations conducted simultaneously from two satellites, Aureol-3 and IKB-1300, over the same earthquake epicenter area prior to the main shock are reported. Of the 20 Aureol-3 flights during which detectable increases were observed in the precipitation of high-energy (greater than 100 keV) electrons and protons, earthquakes of magnitude greater than 4 (Richter scale) were observed in 18 cases at L less than 1.3 from the magnetic equator, with a longitude displacement of +/- 60 deg. And the HAARP program which seems to want to draw inspiration from these mechanisms (up to scales of power and extent): * what it is possible to do with HAARP?. Finally, in the opposite direction, that of an emission of ELF waves from fault zones (piezoelectric rocks that would work), an observation program is still being carried out with the DEMETER (this program is now closed): * Detection of Electromagnetic Emissions Transmitted from Earthquake Regions. Etc |
In short, to discriminate and distinguish between the two mechanisms proposed above, it would be interesting to study whether there is a correlation between variations in solar irradiation and earthquakes at different time scales. To have superficially approached the question, the diurnal and/or seasonal cycles do not seem to have an impact. On the scale of the last 30 years, a weak correlation exists between the increase in temperature and solar irradiation, but it becomes false again on the scale of the century. The correlation could perhaps be relevant with the average temperature variations on the globe, but we diverge from the subject...
But what about the compared risks between earthquakes and the sun?
To answer this question, it is necessary to have a better approximation of the frequency of the events, in particular for high X, which is not the case with the preceding linear approximations. Moreover, you may have noticed that I have not included in these the last value provided for each of the solar risk scales:
- on the one hand these values considerably degrade the correlation coefficients of the various affine equations,
- on the other hand, there are only rare events associated with these "high" values: respectively, for each of the 3 scales, 1, 1 and 5 events counted over a period of 11 years, which statistically is fragile.
However, as we wish to know more precisely the frequencies of the events when these become rare and extreme, it would be fair to try to have a better approximation function for high X. We therefore propose to use a quadratic equation. However, what this equation will make us gain on large X, we will lose it in "general" precision and taking into account the statistical uncertainty on the points added.
We actually check that the correlation coefficients are all (slightly) degraded, except for earthquakes where it becomes equal to 1 (=> the tracking period is longer, the statistics are more reliable, only 4 points are correlated this which with a quadratic equation facilitates the operation!)
Which in the form of a log/log graph gives:
Above right, the colored rectangles indicate the power scales provided by the NOAA (in red/orange/purple) in comparison to the Richter scale: they are very small!
It clearly appears here that events of a solar nature can reach levels of power that greatly exceed the scales designed to follow them . .
Certainly the scales are open, but it seems irresponsible not to make them stick to reality, and not to anticipate the impact that a major solar eruption would be likely to have. Because, if a rough idea of the effects that we can expect according to the power of the events is well provided on the NOAA site, this one is evoked only for events covered by their scales!
As for earthquakes, if the high values of the Richter scale are only rarely reached (or even never on a human scale for powers of order 10, 11 and 12), despite everything, the most powerful events recorded , exceed -with equal frequency- the most remarkable solar events discussed on the web: see the graph below.
Comparison of seismic and solar scales according to the periods associated with their degree of power
For clarity, we can project this information onto a simple graph from the periods:
This result is instructive:
On the scale of even 250 years, the Earth is likely to experience a solar event 100 times more intense than what we have already experienced in the past 20 years, whether in terms of solar radiation or magnetic storms, and of order 10 times higher in X-radiation.
Remember that unlike an earthquake, a solar-type event would have a worldwide impact.










