Corrélation
Définition d'un dictionnaire terminologique: « Les études de corrélation permettent notamment de déterminer s'il existe ou non une association entre deux séries d'observations et d'évaluer l'importance et le sens de cette association (coefficient de corrélation). Par exemple, la corrélation entre le nombre d'appels téléphoniques (x) et les heures auxquelles ils sont reçus (y). »
Sommaire
Coefficient de corrélation
Un coefficient de corrélation est un indice dont la valeur varie entre -1,0 et 1,0 inclus et qui reflète le degré de similitude entre deux séries de données. Nous recherchons donc une relation entre x et y : R(x,y).
Fonction de corrélation
Communément, la corrélation répond à une fonction linéaire où làon exprime y en fonction de x (y=ax+b à) (voir làexemple donné ci-après). Meilleure la corrélation est, plus làindice est proche de 1.
Ceci étant, il này a pas que des corrélations linéaires : les corrélations peuvent être exprimées par une relation polynomiale, exponentielle, sinusoïdale, séries de Fourier, etc.
le calcul dàun coefficient de corrélation (ou dàune équation de régression linéaire) sur des données qui obéissent à une relation autre que linéaire peut induire en erreur en mésestimant le degré de relation entre les variables, voire en suggérant une absence de relation.
Erreur fréquence: une corrélation ne signifie pas que deux variables sont nécessairement synchronisées dans une relation d'amplitude directe
Corrélation et relation de cause à effet
Et, attention, corrélation ne signifie pas relation de cause à effet. Il y a souvent des variables cachées quàil faut identifier, correspondant à dàautres facteurs exogènes à identifier qui pourraient être en relation plus étroite avec le phénomène.
Face à une corrélation significative entre deux variables x et y, il y a trois interprétations possibles:
- Soit la variable x est la cause de la variable y.
- Soit la variable y est la cause de la variable x.
- Soit, le plus souvent, les deux variables étudiées sont influencées par une (ou plusieurs) autre(s) variable(s) exogène(s).
Lorsquàune corrélation (ou régression) peut être attribuée à une variable exogène, on parle souvent de fausse corrélation ou de corrélation absurde.
Pour mettre en évidence une relation de cause à effet, il faudrait pouvoir maintenir constant tout les facteurs exogènes susceptibles dàinfluencer la relation entre les deux variables (ce qui est souvent irréalisable) ou tenir compte de leurs effets dans une régression multiple.
Fausse corrélation
Par exemple, on pourrait montrer quàil y a une corrélation significative entre le nombre de machines à lessiver et la fréquence de làobésité dans la population belge. Cela ne veut pas dire que les machines à lessiver sont la cause de làobésité ou que làobésité stimule làachat de machines à lessiver. Il y a en fait un facteur plus général qui influence simultanément les deux variables. Il sàagit du progrès technologique. Le progrès technologique permet dàobtenir des machines à lessiver à un prix abordable pour la plupart des gens. Mais le progrès technologique généralise aussi les aliments très caloriques tout en réduisant làeffort physique que produisent les gens en moyenne (sédentarité, multiplication des activités peu physiquesà).
Absence de corrélation
D'une corrélaton entre deux phénomènes qui n'aboutit pas, peut quelquefois amener à des résultats inattendus par un mécanisme connu depuis une vingtaine d'années sous le nom de sérendipité.
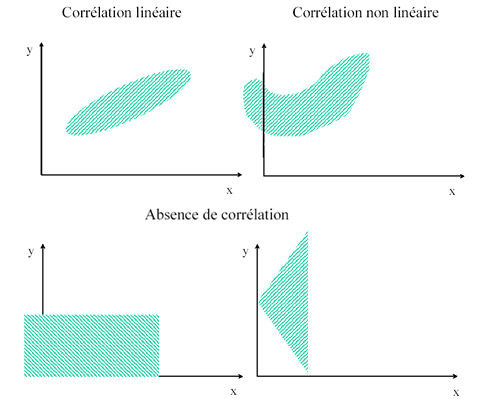
Le nuage de point décrivant la corrélation suit une fonction.