Signal observations
Sommaire
- 1 modélisation du « signal »
- 1.1 Observations, sur 50 ans
- 1.2 Spectre fréquentiel des observations sur 50 ans
- 1.3 Modélisation des fréquences remarquables
- 1.3.1 Classe I : cycles d'événements importants mais de courte durée
- 1.3.2 Classe I.1 : cycles d'événements associés à I, plus persistants dans la durée
- 1.3.3 Classe II
- 1.3.4 Classe III : pics de faible intensité, durée des événements sensible à la fréquence
- 1.3.5 Classe IV.1 : Evénements suspects 1
- 1.3.6 Classe IV.2 : événements suspects 2 (en est-ce vraiment ?)
- 1.4 Reconstruction du signal
- 1.5 Critique de la méthodologie et des paramètres choisis
- 1.6 Modélisation par apprentissage: réseau neuronal
modélisation du « signal »
Nous essayons ici de reconstruire la courbe du signal créé par les observation sur plusieurs dizaines d'années. En s'appuyant sur des harmoniques, il est possible de dégager des fréquences privilégiées.
Les graphiques présentés ci-après et utilisés pour cette étude sont la propriété de Larry Hatch (larryhatch(at)sysmatrix.net) que je remercie. Si vous êtes intéressés, vous pouvez trouver plus d'informations sur son site web:
![]() "*U* UFO Database." Un catalogue de données de 18370 objets, représentant plus de 20 années de recherche {{{Auteur}}}. Accédé le 02/2005 pour cette étude.
"*U* UFO Database." Un catalogue de données de 18370 objets, représentant plus de 20 années de recherche {{{Auteur}}}. Accédé le 02/2005 pour cette étude.
Malheureusement, comme souvent sur les données réalisées par des passionnés, il n'existe aucune information sur la méthodologie mise en oeuvre quand aux méthodes de collecte et d'intégration des informations.
A propos de la consistance de cette base de données
Autres sources de données
Nous prévoyons d'étendre le champ de cette étude à d'autres sources de données, notamment à tous les catalogues librement accessibles, par exemple celui de Luc Chastan. En s'appuyant sur celui-ci nous proposons un modèle partagé d'édition et de vérification des ressources et des connaissances. Ce qui correspond aussi à la mise au point aussi d'un modèle de saisie s'appuyant sur la base de Luc Chastan et accessible ici : UFO:Cases:2A. Nous souhaitons mettre, évidemment, l'accent sur l'environnement proche pour chaque cas étudié (sources d'effets néguentropiques pour le biotope à proximité ou dans la direction empruntée par l'engin).
Qui savait par exemple qu'il y avait une station radar HF non loin de valensole à l'époque ou feu Maurice Masse avait été le témoin d'un atterissage ? Connaissant l'impact possible sur l'environnement/la biosphère que peut avoir un radar HF, le témoignage d'un être penché sur un pied de lavande, peut prendre une perspective radicalement nouvelle.
Méthodologie d'analyse et d'évaluation de l'information
Sur l'information sa cohérence, et la substantialité.
Observations, sur 50 ans
![]() "Nombre d'observations mensuelles." {{{Auteur}}}. Extraction du 01/1946 au 01/1996.
"Nombre d'observations mensuelles." {{{Auteur}}}. Extraction du 01/1946 au 01/1996.
50CLIP.gif © 1985-2005 Larry Hatch
(1 pixel = 1 mois)
Spectre fréquentiel des observations sur 50 ans
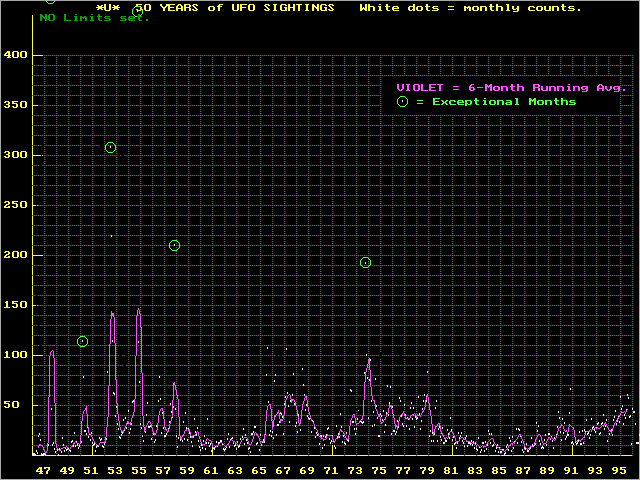
Un graphique réalisé par Jacques Vallée au cours des années 1970 propose visualiser les observations sous formes de fréquences. Le graphique ci-après est également issu du site de Larry Hatch.
![]() "Observations en fréquence." {{{Auteur}}}. Extraction du 01/1946 au 01/1996.
"Observations en fréquence." {{{Auteur}}}. Extraction du 01/1946 au 01/1996.
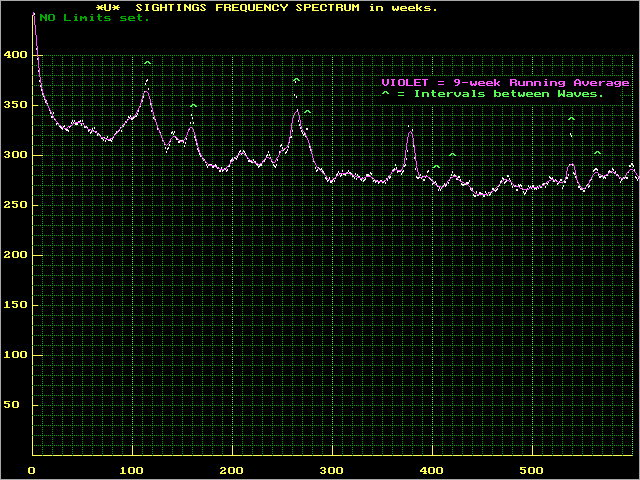
FREQSPC.gif © 1985-2005 Larry Hatch
Voici la légende qui accompagne ce graphique sur le site de Larry Hatch :
"Every UFO sighting in these data is compared to all subsequent listings, regardless of location. A special array is incremented for each interval in weeks elapsed between sightings. Counts for each interval show as white dots. The violet curve is a running average of these counts. As expected, time intervals between major waves show as peaks in this curve, and are marked with a green carat ^ sign. [...]"
Ce graphique montre les vagues les plus caractéristiques avec leurs fréquences propres. La dispersion des observations liée à chaque vague.
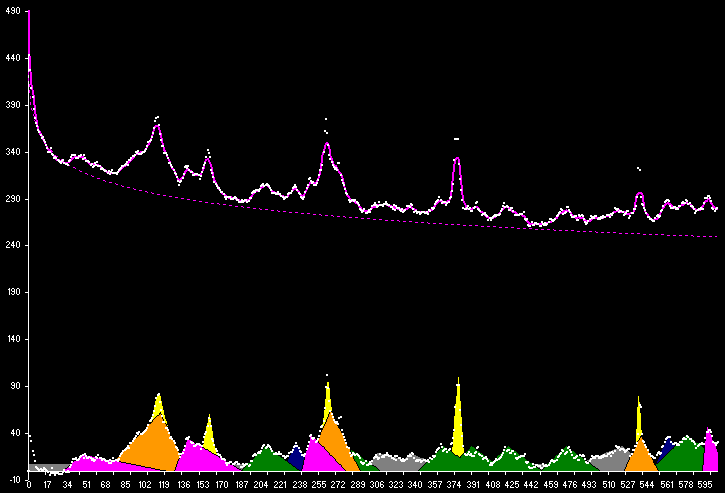
Modélisation des fréquences remarquables
Le graphique en fréquence a été repris afin d'essayer pour extraire un ou plusieurs modèles basés sur une description "fonctionnelle". Notons immédiatement qu'il n'y a pas qu'un unique modèle qui saura convenir. Néanmoins et pour restreindre l'espace de recherche, nous essayons de privilégier les modèles les plus "économiques" possibles en termes de paramètres et afin de modéliser le signal. Un principe de parcimonie que l'on retrouve dans les réseaux neuronaux et qui peut aussi se perçevoir en termes de "compression d'information"... (la structure sous-jacente contenue dans l'information compressée plus le programme permettant de la lire, mais je m'égare...).
Les dispersions statistiques sont normalement caractérisées par des lois normales (ou cf wikipedia). Cependant, dans ce cas, nous observons que les enveloppes semblent difficiles à approximer, notamment pour les "pics d'observation" qui nécessitent un nombre d'individu considérable (n). Ce qui ne semble pas très réaliste aussi, toujours dans le sens d'une certaine "parcimonie", nous avons préféré employer des fonctions linéaires par parties.
Nous suppposons qu'un certain niveau de « bruit » (créé par les canulars, erreurs, etc.) est supportable: la stratégie est de travailler sur un grand nombre de cas (plusieurs milliers) et non seulement quelques uns: ces cas gênants devraient alors être répartis plus ou moins uniformément.
Ci-après une fonction d'approximation linéaire par partie pour l'ensemble des fréquences:
http://www.u-sphere.com/data/FREQXLS.zip
Regroupement des fréquences par classes
Ce regroupement est subjectif dans la mesure où les critères choisis ne s'appuient que sur une ou deux caractéristiques partagées. Ces critères sont indiqués. (Globalement, les regroupements en classes se font par ordre d'intensité (n)).
A chaque classe correspond une "typologie" de phénomènes, s'organisant dans la durée et en intensité de façon précise.
Ci après, nous écrivons:
position (x en semaines) à laquelle le pic est maximal,
ratio correspondant à la vitesse de croissance/décroissance (pente) de l'événénement, n amplitude maximale, y = MAX(-
*|x-
|+n,0) CC : lorsqu'indiqué, le coefficient de corrélation calculé pour la portion de courbe. Les pics sont représentés par des lettres en allant de gauche à droite
60 < n < 100= 1/23*x (0,044*x)
| A: | n = 85 | |
| B: | n = 60 | |
| C: | n = 100 | |
| D: | n = 100 | |
| E: | n = 80 |
40 < n < 60associé à la classe I
+ = 2,5 (vérifier si n est également associé à la classe I)
| A: | n = 63 | ||
| B: | n = 66 | ||
| C: | n = 40 |
remarque 1: cette classe n'est peut-être qu'un artefact lié au choix de l'utilisation de fonctions linéaires par partie et ce au lieu de lois normales (gaussiennes). En effet, les événements rattachés sont temporellement liés à ceux de la classe 1 et correspondent à des durées plus longues: la base est plus "évasée"). Cependant, trois éléments militent contre:
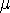 ne dépend pas de x,
ne dépend pas de x,- la forme globale des courbes (1 + 1.1) serait convexe non concave,
- la répartition des points apparait "strictement" linéaire là où elle est visible.
remarque 2: il est tout à fait possible qu'il y ait des événements masqués (car confondus) avec 1.B et 1.D
18 < n < 50 ; (fonction linéairement croissante de x, apparement)+ = 1/200*x (0,0052*x)
- = 1/50*x (0,0208*x)
| A: | n = 18 | |
| B: | n = 35 | |
| C: | n = 40 | |
| D: | n = 50 |
n = 27+ = 9/10 (indépendant de x)
- = 6/5 (indépendant de x)
| A: | ||
| B: | ||
| C: | ||
| D: | ||
| E: | ||
| F: | ||
| G: | n = 39 |
le dernier événement (G) n'appartient peut-être pas à cette classe.
Deux événements qui ne mériteraient pas la création d'une classe à eux seuls...Peut-être est-il possible de les rattacher à la classe I.1 si ce n'est qu'ils ne sont pas en relation avec un événement de I
30 < n < 40+ = 2 (indépendant de x)
- = 2,8 (indépendant de x)
| A: | ||
| B: |
Nous regroupons ici les cas à faible niveau d'intensité, c'est à dire, proche du niveau de bruit de fond (événements ponctuels) évalué à n~8.
n < 30
| A: | n = 20 | |||
| B: | n = 20 | |||
| C: | n = 27 |
Bruit de fond :
| X: | n = 8 |
Reconstruction du signal
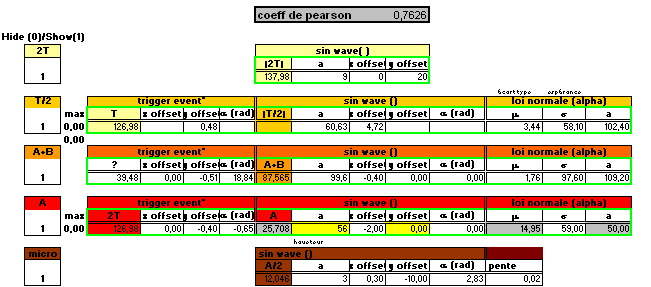
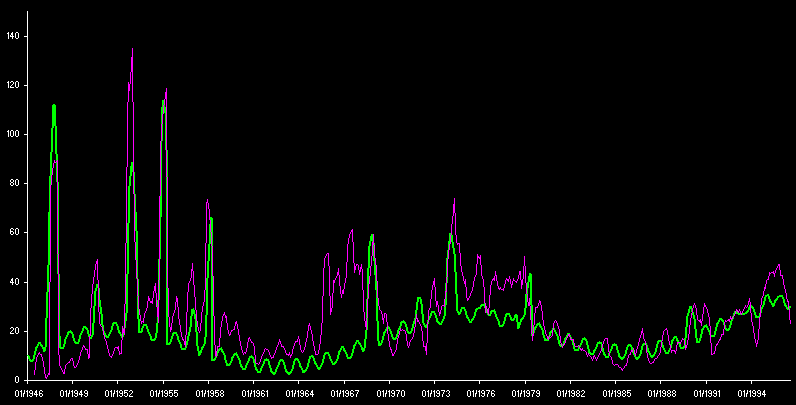
A l’instar d’une décomposition en séries de fourrier, ayant modélisé les « harmoniques » principales nous pouvons reconstruire le signal. Ci-après, la présentation n'est plus en fréquence mais en durée:
- Axe des x: mois écoulés partant du 01/1946. - Courbe violette: la courbe des observations telles qu’issues de la BD de Larry Hatch - Courbe verte: la courbe « corrélée ». - Coefficient de Pearson : ~0.76. Ce qui n'est pas très bon (!), et ce probablement compte tenu du faible nombre de variables pris en compte.
remarque 1:ici ce "pré-travail" ne correspond pas directement à ce qui a été présenté plus haut en termes de paramètres mesurés et dans la mesure où seuls ici 4 paramètres principaux sont retenus.
Un travail exhaustif reprenant l'ensemble des fonctions linéaires approximées précédemment sera réalisé dès que je pourrais.
remarque 2: la courbe de corrélée s’appuie essentiellement sur la période du soleil (T) et deux autres paramètres A et B (avec B~T/2). Il s’agit de somme de sinusoïdes et de lois normales de répartition s’exprimant sur ces sinusoïdes sur des fréquences précises (moyennant l’application de certains offsets en x & y).
Critique de la méthodologie et des paramètres choisis
Nous soulevons des biais expérimentaux, liés à :
- la qualité de la base de données:
- la validité des informations collectées,
- la réalité non réductible simplement des phénomènes observés,
- l'exhaustivité des informations collectées.
Ces biais sont conditionnés par la qualité du matériel expérimental utilisé. D'où, l'extrême importance qu'il faut y accorder.
[autres biais :...]
Modélisation par apprentissage: réseau neuronal
De façon amusante, une modélisation semble tout à fait possible par l'utilisation d'un réseau neuronal.
Nous proposons d'approximer le signal ci-dessus, à partir d'un réseau neuronal.
Il y a un côté arbitraire dans le choix du RN (couches, neurones, fonctions de transfert), qu'il doit être ultérieurement possible de corréler à des variables environnementales.