« LAC CHAUVET » EGLISENEUVE-D’ENTRAIGUES (63) 18.07.1952
Le vendredi 18 juillet 1952, à 18:10, André Frégnale, ingénieur géologue, se promène à pieds près du lac Chauvet (Puy-de-Dôme). Il fait très beau temps, le ciel est bleu azur avec un fort vent d'ouest.
Sommaire
Le témoignage d'André Frégnale
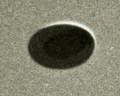
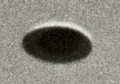
"Il était environ 18 heures, a raconté M Frégnale, lorsque j'ai aperçu la soucoupe. Ignorant sa circonférence, je ne peux pas dire à quelle altitude elle volait. Apparemment elle se trouvait entre 3.000 et 8.000 mètres. Je ne pense pas que l'altitude ait pu être plus élevée, car alors, en raison de l'épaisseur de l'atmosphère, l'engin aurait présenté une teinte métallique bleuté qu'il n'avait pas.' Quatre clichés. "J'ai eu le temps de prendre quatre clichés très rapidement. J'ai vu l'engin environ pendant 50 secondes et après avoir pris les vues j'ai observé l'engin à la jumelle. D'après mes observations et les calculs que j'ai fait par la suite, si la soucoupe se trouvait à 3.000 mètres elle se propulsait à environ 300 mètres à la seconde. Si elle se trouvait à 8.000 mètres sa vitesse était naturellement plus grande et pouvait atteindre 800 mètres à la seconde. Je n'ai entendu absolument aucun bruit. "L'engin - comme on l'a dit souvent - à la forme d'une soucoupe ovale. En dessous et au centre il semble qu'il existe un léger renflement, mais je n'en suis pas certain. Autour de la partie circulaire apparaît un cercle brillant. Je suppose qu'au-dessus de l'appareil des pales, ou quelque autre système gyroscopique, tournent très rapidement, ce qui expliquerait le reflet que l'on voit très nettement sur les clichés que j'ai pris." Le témoin utilise un appareil photo qu'il porte sur lui, un 24x36 Zeiss Ikonta équipé d'un objectif de 45 mm. Il prend 4 clichés, pendant 25 s. (source?) Lorsque l'engin est trop loin pour le photographier correctement, Le témoin prend ses jumelles pour suivre l'objet qui s'éloigne et le voit disparaître, quasi instantanément, comme s'il s'évanouissait sur place. Au total, l'observation a duré moins de 1 mn. (source?) Le témoin aurait cependant toujours refusé de croire en la réalité des ovnis, et pour ce qui est de l'objet qu'il a photographié, pense qu'il peut s'agir d'une maquette volante, ou - plus étonnamment pour un témoin direct - de poussière cosmiques agglomérées (sic).
- Quotidien le Méridional, France, p1 et p8
- Informations Pathé
(sources à préciser)
Qu'en penser ?
Difficile, après plus de soixante années passées, d'expertiser des négatifs qui ont de toutes façons disparu et pis encore, d'interroger un témoin maintenant décédé. Intéressant de constater selon les mots du témoin l'esprit critique qu'il a vis à vis de l'évaluation des dimensions, piège dans lequel tombent pourtant de nombreux témoins aujourd'hui.
Pourtant, les photos prises au Lac Chauvet apparaissent toujours aussi intrigantes, trop belles pour être vraies selon certains: la question du "quoi ?" reste toujours posée.
D'une part, avec le recul, malgré la propre prise de distance du témoin, cela ne pourrait-il pas être canular ? Frégnal aurait t-il pu volontairement photographier un objet lancé ou planant ? D'autre part, Pierre Guérin, professeur à l'institut d'astrophysique de Paris, avait publié plusieurs analyses de ces photos, concluant à leur authenticité. Cependant il est parti d'un postulat : la trajectoire était rectiligne, plaquant son analyse sur les propos du témoin, et donc sa sincérité.
Sceptiques et croyants sont montés à l’assaut, régulièrement, pour réfuter et prendre position. Je préfère vous prévenir immédiatement: je ne mettrai pas un point final à cette affaire, je préfère juste modestement une contribution. Sommaire
Méthode d'analyse
Sans remettre en cause les propos du témoins, mais sans non plus s'appuyer sur ceux-ci, je trouvais intéressant l'idée de modéliser la trajectoire en 3D, uniquement sur la base des photos: peut-on vérifier si les mots du témoins sont en accord avec les photos ? D'autant qu'en parcourant le net, je n'ai nulle part retrouvé de tentative de reconstitution de la scène permettant de se représenter le cadrage et la trajectoire (si ce n'est sous forme d'équations et paramètres trigonométriques).
J'ai décidé de travailler en "aveugle", c'est à dire, sans reprendre les éléments de calcul de Pierre Guerin, ni ceux présentés sur le site d'Adelmon pour essayer de rester aussi "neutre" que possible.
Pour recréer un modèle tridimensionnel de la scène, je me suis appuyé sur un outil que j'utilise de temps en temps, qui me permet de retrouver les paramètres de géométrie en 3D sur des objets que l'on voit en photo. Ici, je l'ai un peu fait évoluer de façon à ce qu'il tienne compte simultanément des 4 photos et propose une reconstitution dynamique de la scène, en fonction des paramètres entrés.
Mon objectif était de trouver au moins une configuration pouvant satisfaire aux photos et aux conditions d'éclairage.
Détermination de l'orientation du phénomène et de ses contours
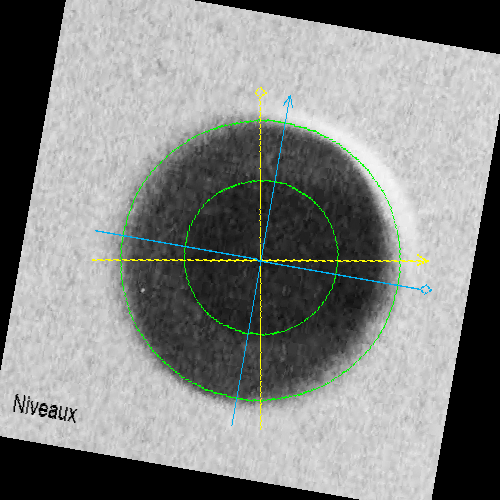
Compte tenu du flou de bougé, pour aider à détertminer les limites de l'objet sur la photo, mais aussi pour déterminer ses paramètres d'orientation dans l'espace, je suis parti du principe qu'il s'agissait d'un disque en 3D. Plus précisément, un modèle à base de deux disques, dont celui central est situé très légèrement au-dessus de l'autre: j'ai tenu compte d'une très légère asymétrie des centres respectifs. Elle parait correspondre à un "enfoncement" du disque central, d'ailleurs moindre que celui d'un modèle 3D de pigeon d'argile (~1 % en proportion du diamètre, peut-être considéré comme négligeable et nécessite de meilleurs photos pour trancher).
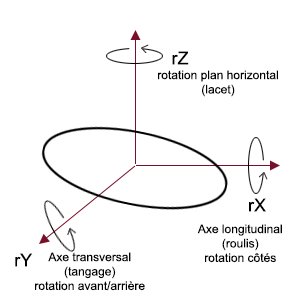
J'ai visualisé ce disque dans l'espace à "plat" , puis, j'ai utilisé 3 axes de rotation selon un repère attaché à ce disque 3D, pour en faire varier l'affichage.
Grâce à cela, en jouant sur les 3 axes de rotation nous faisons varier la position de la forme 3D dans l'espace jusqu'à retrouver la configuration exacte de chaque photo.
Ce sont les valeurs rX, rY et rZ (exprimées en degrés) utilisées sur la page du simulateur (présenté plus bas dans l'article) que j'ai enregistrées et que vous pouvez modifier. J'applique également un coefficient de zoom (Zoom Factor) qui permet de déterminer la taille angulaire du PAN sur chaque photo.
Utiliser une même forme 3D pour chaque photo permet d'aider à réduire les incertitudes d'une photo sur l'autre, comme par exemple, sur la position de la zone sombre centrale, plus nette sur la photo 3, que l'on peut du coup recaler/retrouver plus aisément sur les autres.
Détermination de la position du phénomène dans l'espace
L'approche a été la suivante: dans un premier temps, je ne me suis appuyé que sur les angles relatifs PAN/soleil/observateur pour ne pas être parasité par les orientations des photos. Quelle que soit la position du photographe et l'inclinaison de ses photos, ceci ne devait pas avoir d'impact sur le rendu du phénomène en tant que tel.
En effet, il existe toujours au moins deux repères visibles sur chaque photo du phénomène qui permettent de délimiter un arc lumineux le long du phénomène. Ils sont liés à la réflexion de la lumière sur la surface de l'objet et ils sont notés dans le schéma ci-dessous par une croix orange et bleue.
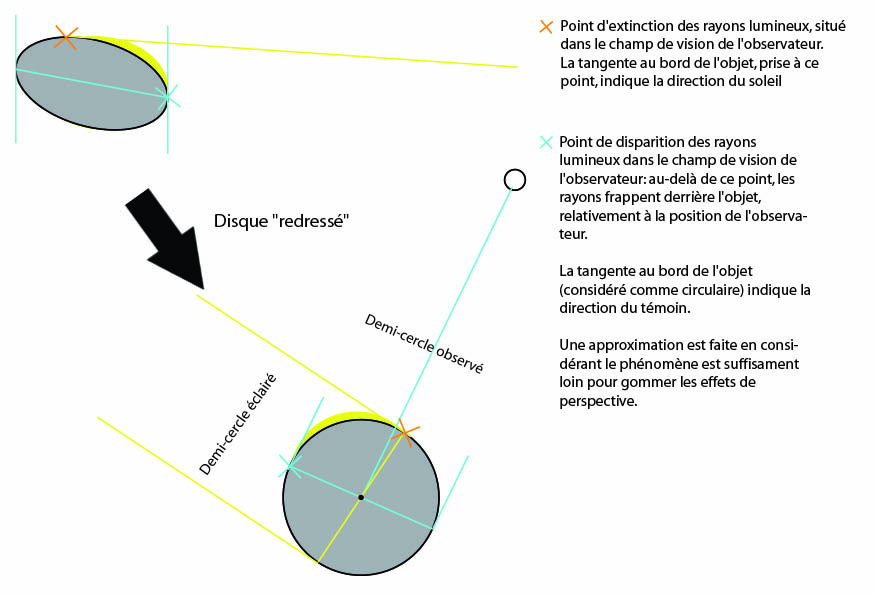
• La croix bleue représente le point de disparition des rayons lumineux, dans le champ de vision de l'observateur. Au-delà de ce point l'observateur ne peut plus les voir car les rayons lumineux bien réfléchis mais, sont derrière l'objet, relativement à sa position. En utilisant ce point de disparition, et en prenant la tangente au bord de l'objet on doit retrouver la direction de l'observateur.
Application de la méthode
Partant de cette idée, il me fallait les moyens de calculer ces tangentes et donc de redresser les formes en choisissant les bon paramètres de géométrie 3D. De façon classique, le programme que j'ai réalisé utilise des rotations suivant les 3 axes x, y, z, et en considérant que le repère formé par les axes (x, y, z) passe par le centre de l'objet.
Un simulateur 3D pour trouver les paramètres d'inclinaison du phénomène
Vous pouvez tester le programme (vous ne casserez rien ! des paramètres par défaut sont enregistrés, ils sont remis automatiquement à chaque usage).
J'ai essayé de faire en sorte que ce soit assez ludique, et que tout le monde puisse essayer de déterminer des paramètres qui fonctionnent.
Comment appliquer les paramètres de prise de vue
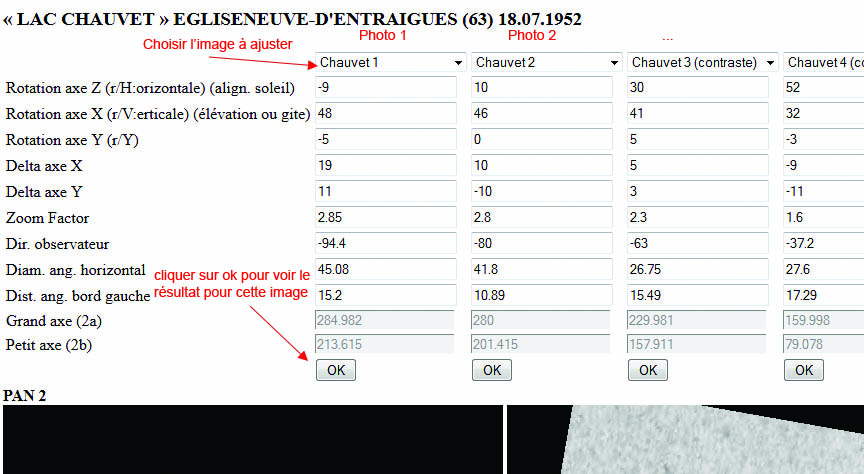
Lorsque l'on se connecte sur la page, voici comment cela marche:
- d'abord, on choisi la photo sur laquelle on veut travailler et on appuie sur "OK",
- ensuite, les cercles verts doivent être alignés sur les contours extérieurs et intérieurs des photos du phénomène, avec l'incertitude liée à la nature du biseau sur le bord de l'objet et du flou
- puis, la croix jaune permet de trouver la direction du soleil. Il faut aligner le losange jaune sur le point d'extinction de la lumière. La flèche jaune indique alors la direction du soleil. La croix jaune (l'éclairage de la surface) est solidaire de l'objet 3D. Il faut faire varier le paramètre "Rotation axe Z"
- enfin, la croix bleue permet de trouver la direction du témoin. Cette fois-ci, il faut aligner le losange bleu, sur le deuxième point d'extinction de la lumière, là ou elle disparait pour passer derrière le phénomène. Il faut jouer sur le paramètre "Dir. observateur", indépendant des paramètres de visualisation 3D de l'objet. A noter je pense qu'ici vous pouvez aussi rechercher l'intersection avec le point qui détermine la plus grande largeur apparente de l'ovale: si la photo est bien horizontale cela devrait être équivalent (cf. schéma précédent).
Enfin, vous pouvez jouer sur les autres paramètres :
Et quand vous êtes satisfaits, vous validez à nouveau sur le bouton [OK]: une photo redressée est calculée avec les paramètres donnés, sur celle-ci apparaissent la direction du soleil et du témoin :
Ces directions permettent de positionner le phénomène sur un plan 2D: ce qui compte c'est que l'écart relatif entre les flèches jaunes et bleues soient conservé. J'ai considéré de façon également arbitraire que l'élévation était donnée par la rotation rX.
La distance effective au témoin est relative à la taille du phénomène (en mètres), qui est également arbitrairement donnée : vous pouvez la modifier pour simuler un objet aussi grand/petit que vous souhaitez. Cela ne changera pas l'orientation et la géométrie générale.
D'autres paramètres sont accessibles: direction du soleil, résolution angulaire des photos, distance angulaire du centre des phénomènes relativement au bord gauche de chaque photo.
Ci-après, le trait blanc, représente un exemple de trajectoire dynamiquement calculée. Les arcs violets sont les champs angulaires des photos (redressées horizontalement).
A noter que quand vous appliquez les paramètres de rotation ceux-ci sont effectués dans l'ordre suivant :
1. rotation autour de l'axe Z (dans le plan horizontal), 2. rotation autour de l'axe X (qui correspond à une inclinaison latérale, gite ou élévation sur l'horizon) à 90° cela équivaut à voir le phénomène au zénith, et enfin, 3. rotation sur l'axe Y vers l'avant ou l'arrière (cambrure en quelque sorte).
Conclusions
Les conclusion ci-après ne sont bien entendu pas définitives. Toutefois, voici ce que l'on peut dire partant de cette proposition de reconstitution :
- s'il s'agit bien de la même série de photos et du même phénomène, il a effectivement une trajectoire "relativement" rectiligne
- l'altitude est à peu près constante : légèrement "creusée" au début par une descente sensible jusqu'au point 2, puis remontée légère jusqu'au point 4
- la zone sombre est orientée dans l'axe du soleil, sauf sur la photo 3 et 4 un décentrage d'une dizaine de degrés se produit, dans le sens du déplacement.
- il s'en faut de peu pour que les photos 3 et 4 se superposent (mais ça on le savait).
Je me suis demandé si la radiosité pouvait expliquer la zone sombre visible sous le phénomène (http://fr.wikipedia.org/wiki/Radiosit%C3%A9_%28infographie%29), puisque cette zone est orientée dans l'axe du soleil. (Particulièrement sur les photos 1 et 2, mais c'est un peu moins vrai pour la 3 et la 4). En effet, peut-être la tranche du phénomène masquait le soleil et créait une ombre sur sa face intérieure ? L'éclairage de la face inférieure, n'aurait alors était du qu'à la radiosité (un éclairage indirect depuis le sol). J'ai réalisé un modèle 3D sur la base d'un disque de type "pigeon l'argile", et si l'on peut s'approcher de l'effet escompté jusqu'à un certain point: il faut que la lumière ambiante soit beaucoup moins forte, qu'il fasse presque nuit: avec un éclairage à 18:10 locale (17:10 TU), c'est beaucoup trop clair, de plus, dans sa partie descendante (1 et 2), le phénomène est incliné vers le soleil; il ne joue pas le rôle de "parasoleil", à l'inverse du modèle que j'ai fait ici :
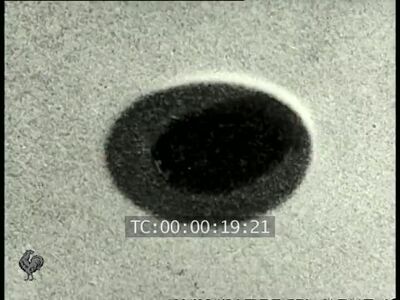
De plus, même avec un ciel plus sombre, je n'arrive pas à prolonger l'ombre jusqu'au bord du phénomène: il y a toujours un contour plus clair, au contraire de ce qui apparait sur l'image du film Pathé (1921.jpg en PJ).
Alors est-ce que cette zone sombre est constitutive du phénomène ? Probable. Elle apparait également dégradée: le noir semble aller en s'éclaircissant vers la partie arrière (voir la coupe radiométrique avec IPACO).
Enfin, j'ai pu, en modifiant les paramètres d'URLs sur le site de Pathé, accéder à des photos en grand format normalement cachées et extraites de ce film. Je vous joins les deux plus remarquables:
- Celle ou Fregnal (2207) décrit son observation devant les caméras et qui permet de voir le paysage, notamment une petite montagne boisée en arrière plan, regardant en direction de sa première photo . A vue de nez, je le situerai ici dans la pente : Lat 45.460869, Lon 2.848735, en regardant vers le sud.
- Celle très agrandie du PAN 3 (1921). La zone sombre se détache nettement.
Si vous avez une meilleure série de photos que la mienne, je les ajouterai au logiciel. Peut-être aussi avez-vous obtenu une copie du film sur les archives de Pathé ? J'en ai fait la demande, le cas échéant je suis preneur.
Enfin, voici un photomontage avec les caractéristiques du modèle 2D ci-dessus:
Questions en suspend
- Quel est le point visible sous l'objet dont parle P. Guérin ?
- Il faudrait récupérer le film de Pathé
Remarque importante
Vous l'aurez peut-être noté, mais il existe un espace d'hypothèses possibles pour la reconstitution 3D. Le schéma ci-dessus n'est qu'une configuration possible.
En effet, une inclinaison latérale du phénomène peut-être compensée par une modification de son élévation (hauteur sur l'horizon). Rien ne permet de distinguer ces deux paramètres sans disposer d'une mesure de l'élévation sur l'horizon. Or, ici, seule la dernière photo permet de faire directement ce calcul, sachant que la situation est celle d'une crête vallonnée : le calcul est délicat... Une autre méthode consisterait à partir du film de Pathé, qui laisse à voir une reconstitution avec Frégnale au pied de l'arbre. L'arbre est lui même reconnaissable, là aussi il faudrait utiliser de calculs pour, moyennant une prise de vue différente, retrouver l'élévation théorique. Références
↑ Pierre Guérin, « A Scientific Analysis of Four Photographs of a Flying Disk Near Lac Chauvet », Journal of Scientific Exploration, vol. 8, no 4, 1994, p. 447-469.